Условие: На рисунках (1-4) изображён куб и три точки, размещённые или в его вершинах, или на серединах его рёбер. Установите соответствие между каждым рисунком (1-4) и наименование фигуры (А-Д), получающейся в сечении.

А. треугольник
Б. прямоугольник
В. трапеция
Г. пятиугольник
Д. ромб
Решение
Приведём построение сечения для каждого из случав:
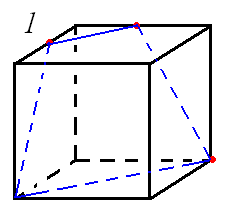
Отрезок сечения в верхней грани будет параллелен диагонали верхней грани, следовательно, и нижней. Значит, плоскость сечения параллельна диагонали нижней грани. При этом одна точка диагонали нижней грани принадлежит сечению. Следовательно, плоскости сечения будет принадлежать вся диагональ нижней грани. В сечении получится трапеция (В)

Самый простой случай – т.к. в каждой грани по две точки, достаточно их соединить и получить теругольник (А)

Точки нижней грани куба, принадлежащие сечению, находим, продлевая рёбра куба и известные прямые, лежащие в сечении. Т.к. данные нам точки лежат на серединах сторон, то прямая, по которой пересекаются плоскости сечения и нижней грани, пройдёт через вершину куба. Таким образом мы получим четырёхугольник с равными сторонами. Это будет ромб, а не квадрат, т.к. одна его диагональ будет равна диагонали куба, а другая –диагонали грани куба. (Д)

По свойству параллельных плоскостей находим обе прямые, по которым плоскость сечения пересекает вертикальные грани куба, и затем находим прямую, лежащую в верхней грани куба. В сечении – прямоугольник (Б)
Ответы:
1. (В)
2. (А)
3. (Д)
4. (Б)
Хорошие задачи! На пространственное восприятие)
ОтветитьУдалить